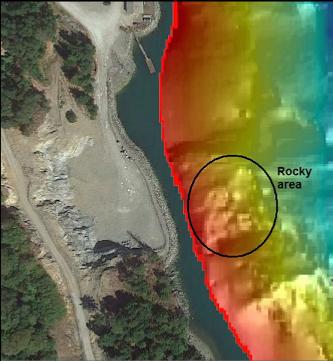
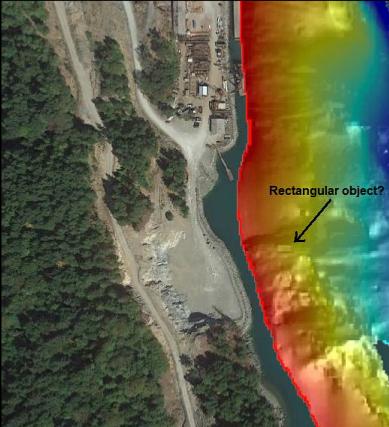
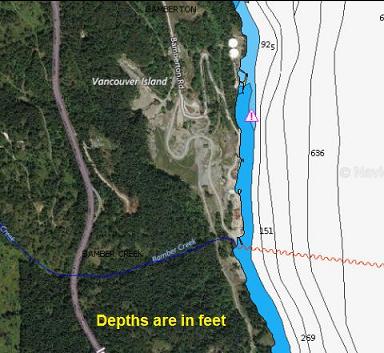
Awhile ago I was looking for things that might be man-made objects on the side-scan image off the site of the old Bamberton cement factory. I saw a rectangular object about 50' long on the Southern end of the site. The sidescan image is such a low resolution that the rectangle could just be a few pixels coincidentally perfectly lined up with each other. If it was man-made, it was too small to be a barge. I thought it could be a sunken dock. Lately I had forgotten about it since I figured it was probably nothing. Today (July 9, 2017) I was looking for somewhere to take my boat for a dive in Saanich Inlet and I thought I might as well have a look for the rectangular object. If it was nothing, the sidescan image also showed a large rocky area nearby that might make the dive interesting anyway.
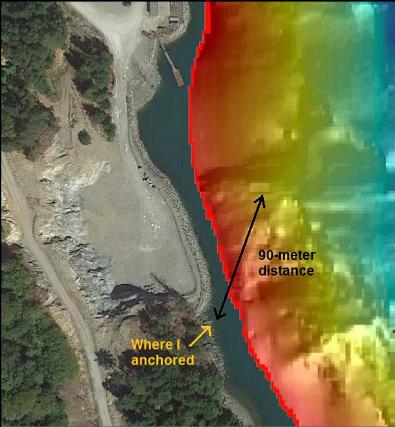



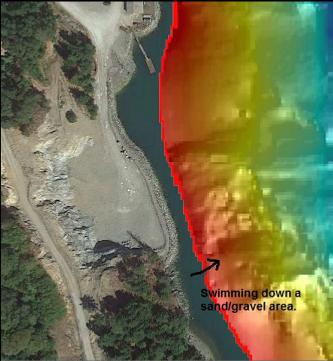

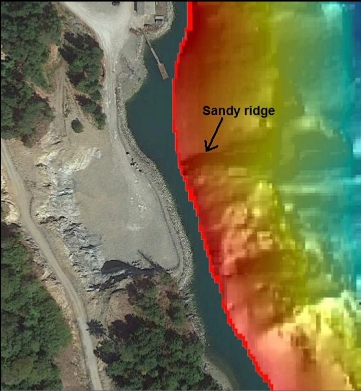
I anchored up near the beach and swam down the slope. Visibility in the shallows was a pretty decent 20', but between 20-40' deep, there was a layer of bad visibility full of floating bits of plankton. Near where I anchored, the slope was sand and gravel.
I soon saw the rocky area shown on the sidescan image. Below about 50' deep, visibility was about 40'. There was a long, yellow plastic spill containment boom stretched out along the bottom. There was an average amount of brown, copper, quillback and yellowtail rockfish. I swam North about 80-100' deep.
My camera strobe decided to stop working (later I saw the circuit board was burnt and the flash tube was broken) so the rest of the photos were taken with natural light.
The rocky area ended and I kept swimming across a sandy area. There was a sudden ridge-like rise where the sand rose up in a mound. I think this is visible in the side-scan image. If so, I had already passed the rectangular object I was looking for. Nearby on the sand there was a smaller rectangular object maybe 60-80' deep (I can't remember exactly). This definitely wasn't the object on the sidescan image since this one (whatever it was) was only about 6' long.
I swam back towards my boat a bit shallower this time (50' deep) to see if I was originally too deep to find the rectangular object I was looking for. I still saw no sign of it.
I ascended back up into the shallows without seeing any sign of a large rectangular object. I try to convince myself that it was just random pixels after all, but I still wonder if I was just swimming at the wrong depths or looking the wrong way when I swam by it.